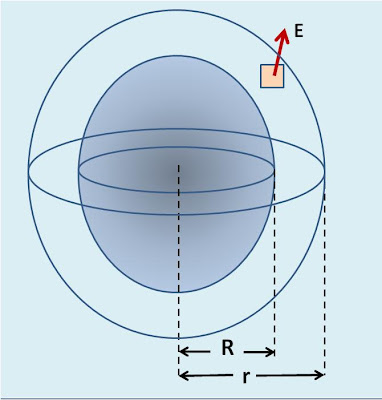
Similar to problem 3.25 since the charge distribution is isotropic (spherically symmetric), the direction of electric field at any point in space will be radially outwards. Consider a Spherical Gaussian Surface concentric with the charged sphere with a radius r. The electric field E will have the same magnitude at all points on the sphere. Further suppose that the charge of the charged central sphere is q.
Similar to 3.25 the total charge contained in the surrounding volume between the Gaussian Sphere and the charged central sphere is given by,

The total charge contained in the Gaussian Sphere is thus given by,

Using Gauss Law now we can compute the electric field as,

It is clear from (3) that when,

then independent of r,

Why are you integrating from R to r why not from R to r-R ??
ReplyDeleteBecause u are taking the limits as the distance from the centre of sphere
ReplyDelete